Kakuro-puzzels oplossen

In deze gids bieden we een reeks praktische tips voor het oplossen van Kakuro-puzzels, met moeilijkheden variërend van beginner tot expert.

Om de regels samen te vatten: Kakuro is een puzzelspel op een kruiswoordraadselachtig bord waarbij cijfers worden gebruikt om ze te laten optellen tot waarden die zijn gespecificeerd in de definitievierkanten van het bord. Bovendien kan binnen elke somgroep elk cijfer maximaal één keer voorkomen.

De traditionele manier om een Kakuro-puzzel op te lossen is incrementeel: door gebruik te maken van de bestaande informatie op het bord, kun je met zekerheid de waarde van een specifieke cel vinden die maar één mogelijke waarde kan aannemen. Vervolgens wordt die waarde gevuld en wordt het proces herhaald totdat alle cellen van het bord zijn ontdekt.

In sommige situaties is er geen specifieke bordcel met maar één mogelijkheid. In die gevallen moeten alle mogelijkheden op zichzelf worden verkend en door middel van tegenstrijdigheden worden geëlimineerd totdat er nog maar één manier van handelen overblijft.

Hieronder presenteren we verschillende methoden om vooruitgang te boeken bij het oplossen van de eigenlijke puzzel.

Unieke bedragen voor specifieke definities

Er zijn enkele definities die alleen op een specifieke manier kunnen worden opgelost:

de som 3 (verdeeld over twee cellen) is altijd 1 + 2.
de som 4 (verdeeld over twee cellen) is altijd 1 + 3.
de som 17 (verdeeld over twee cellen) is altijd 8 + 9.
de som 6 (verdeeld over drie cellen) is altijd 1 + 2 + 3.
de som 24 (verdeeld over drie cellen) is altijd 7 + 8 + 9.

en ga zo maar door... Gewoonlijk kunt u de muisaanwijzer op een Kakuro-raster boven het definitienummer plaatsen en er verschijnt een tooltip met alle mogelijkheden om die som met unieke cijfers in het aantal beschikbare cellen te schrijven.

De sommen die op een unieke manier kunnen worden geschreven, zijn meestal lage of hoge sommen, waarbij lage/hoge cijfers in het antwoord worden ingevoerd om ze te verkrijgen.

Het helpt om een unieke manier te hebben om de som te schrijven, maar houd er rekening mee dat alle permutaties geldig zijn en dat je nog steeds moet uitzoeken welke daadwerkelijke permutatie je op het bord moet gebruiken.

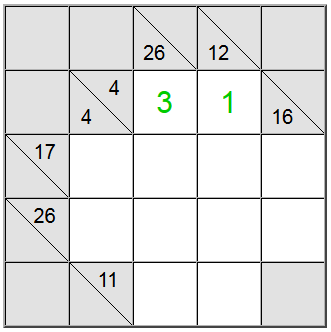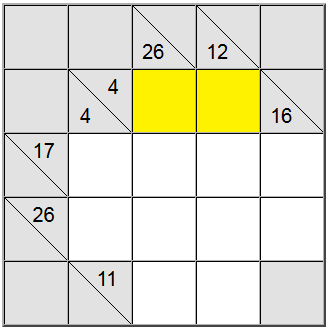
Beperkingen voor rijen en kolommen

Voor de gele cellen die hierboven zijn gemarkeerd, is er maar één manier om de som te schrijven: 4 = 1 + 3. We moeten echter nog uitzoeken welke permutatie (1 + 3 of 3 + 1) we moeten gebruiken.

Blijkt dat de verticale definitie 26 ons helpt: een som in 4 cellen die het cijfer 1 zou bevatten, zou maximaal 1 + 9 + 8 + 7 = 25 zijn. Aangezien onze som 26 is, blijkt dat het cijfer 1 geen deel van de som kan zijn. Daarom is de enige resterende volgorde voor de gele vierkanten 3 + 1.

Definities: kruispunten

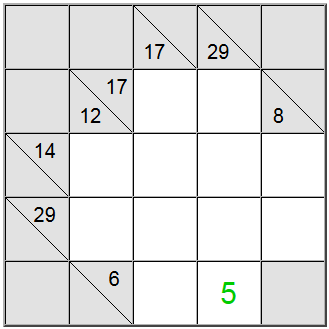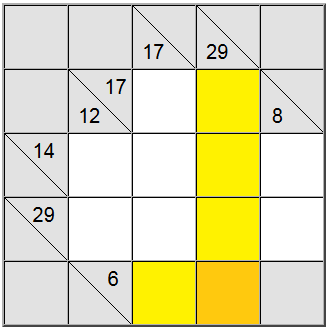
Op het bord hierboven kunnen de horizontale gele vierkanten geschreven worden als 6 = 1 + 5 of 6 = 2 + 4. De verticale gele som kan alleen geschreven worden als 29 = 5 + 7 + 8 + 9.

Het gele vierkant op het snijpunt van deze twee somdefinities moet hetzelfde cijfer bevatten, dus er moet een gemeenschappelijk cijfer aanwezig zijn in de horizontale en verticale definities om tussen beide definities te kunnen worden gedeeld. Door naar de bovenstaande mogelijkheden te kijken, kunnen we er gemakkelijk achter komen dat 5 het enige cijfer is dat aan dit criterium voldoet.

Deze techniek werkt vooral goed bij het kruisen van een lage som met een hoge somdefinitie. Definities van lage som en hoge som zijn de definities die een relatief laag of hoog somdefinitienummer hebben (respectievelijk 6 en 29 voor ons voorbeeld) in vergelijking met het aantal beschikbare cellen. Omdat 6 relatief laag is, worden lage cijfers in de somweergave geforceerd en 29 hoge cijfers (om deze sommen te bereiken met behulp van het gegeven aantal cellen). Daarom bevat de kruising van lage en hoge cijfers waarschijnlijk slechts één kandidaat voor de werkelijke celwaarde.

Min/max-waarden voor een somgroep

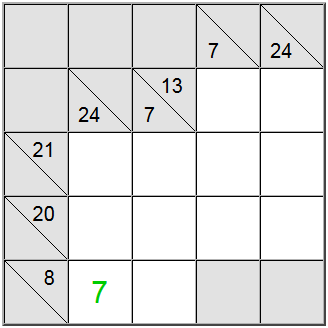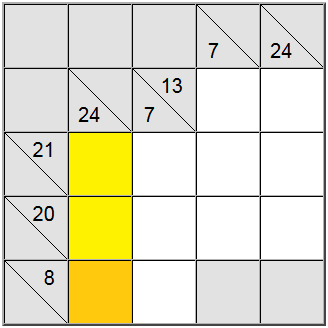
Soms is het handig om de maximale of minimale waarde voor een somgroep te berekenen. Dit kan je een idee geven van wat het geldige cijferbereik is voor dat specifieke bedrag, wat je weer zal helpen om een verband te leggen met andere beperkingen en de unieke opdrachten op het bord te achterhalen.

In het bovenstaande voorbeeld accepteren de gele verticale cellen alleen waarden gelijk aan 7 of hoger. Als je probeert een 6 toe te wijzen, kun je er gemakkelijk achter komen dat 6 + 9 + 8 = 23, zodat de definitiesom van 24 niet haalbaar is.

Omdat 7 een minimum is, dwingt de horizontale definitie met 8 als som de 7 in die positie.

Conclusie

Oefenen is de beste manier om te zien hoe dit advies kan worden toegepast in echte Kakuro-spellen. Speel een echte puzzel. We wensen je veel succes en veel plezier!

Speel Kakuro